Gunnar Morling launched One Billion Row Challenge (1BRC) in the beginning of the year. The goal is to calculate temperature aggregates (min, max, sum) of weather stations. The data is one billion rows of measurements in <string: station>;<double: temperature> format.

Hamburg;12.0
Bulawayo;8.9
Palembang;38.8
St. John's;15.2
Cracow;12.6
Bridgetown;26.9
Istanbul;6.2
Roseau;34.4
Conakry;31.2
Istanbul;23.0

The station names are arbitrary length strings and temperatures are of X.XX or XX.X formatted double values.

Submitted solutions were golden, there were many interesting, optimized submissions. I enjoyed reading them and trying to understand how they work and why they are fast. If only they were easier to understand :-)

Parsing

One of the tasks is to parse the input data, separate station name and its temperature value. For that we have to find the location of semicolon ';' in the each input line!

private static final byte SEMICOLON = ';';

private int findSemicolonPosition(byte[] line) {
    for (int i = 0; i < line.length; i++) {
        if (line[i] == SEMICOLON) {
            return i;
        }
    }
    return -1;
}

Linear scan to find the semicolon position in byte array

Apparently, simple task of finding a byte character in a given string could be heavily optimized.

In this blog I am going to look into two options that were used in 1BRC submissions, the first is “SIMD Within A Register (SWAR)” technique, and the second is to use Java Vector API. Both of these techniques take advantage of processing multiple data on a single instruction.

SWAR

SWAR is technique to process multiple bytes at once taking advantage of 64-bit processor CPU architectures.

The idea is to load multiple bytes into single 64-bit register and then perform bitwise operations to find the index of the matching byte. On little-endian machines, we want the index of the first matching byte from the right end of the register, since little-endian machines reverse the bytes when a word is loaded into a register.

Mainly we are looking for the following function, indexOfFirstMatched(word, pattern):

                                      /
                                     /  0, word = XXXXXXXXXXXXXXOO
                                    |   1, word = XXXXXXXXXXXXOONN
                                    |   2, word = XXXXXXXXXXOONNNN
                                   /    3, word = XXXXXXXXOONNNNNN
indexOfFirstMatched(word, 0xOO) = <     4, word = XXXXXXOONNNNNNNN
                                   \    5, word = XXXXOONNNNNNNNNN
                                    |   6, word = XXOONNNNNNNNNNNN
                                    |   7, word = OONNNNNNNNNNNNNN
                                     \  8, word = NNNNNNNNNNNNNNNN // return byte length
                                      \                            // if no match is found

The OO denotes the match byte, NN denotes a nonzero byte, and XX denotes a byte that maybe zero or nonzero. If no match is found, the function returns the length of word.

This technique perfectly fits for finding locations of semicolons in 1BRC problem during parsing of each line. Most of the submissions used technique from Richard Startin’s “Finding Bytes” blog post.

For example, Thomas Würthinger early submission (slightly modified by me):

private static int findDelimiter(long word) {
    long input = word ^ 0x3B3B3B3B3B3B3B3BL;
    long match = (input & 0x7F7F7F7F7F7F7F7FL) + 0x7F7F7F7F7F7F7F7FL;
    match = ~(match | input | 0x7F7F7F7F7F7F7F7FL);
    return Long.numberOfTrailingZeros(match) >>> 3;
}

However, there is improved version of above approach that works in little-endian architectures. An example of this is from Roy van Rijn early submission (slightly modified by me):

private static int firstAnyPattern(long word) {
    final long match = word ^ 0x3B3B3B3B3B3B3B3BL;
    long mask = (match - 0x0101010101010101L) & ~match & 0x8080808080808080L;
    return Long.numberOfTrailingZeros(mask) >>> 3;
}

Both of these methods find the index of first byte in the 64-bit long word that matches the semicolon ';' pattern encoded as 0x3B3B3B3B3B3B3B3BL.

To learn more why this works, please read Richard Startin’s explanation and check the visuals from Wojciech Muła’s “SWAR find any byte from set” post.

Finding 0-Byte

These optimizations are used in many applications that need to find the index of '\0' — characters in strings. The strlen function in C, instead of checking each byte separately, could load multiple bytes as word to check for the matching byte pattern.

The early versions of the SWAR algorithm was presented by Leslie Lamport in his paper titled “Multiple byte processing with full-word instructions” in 1975.

It’s a neat hack, and it’s more useful now than it was then for two reasons. The obvious reason is that word size is larger now, with many computers having 64-bit words. The less obvious reason is that conditional operations are implemented with masking rather than branching. Instead of branching around the operation when the condition is not met, masks are constructed so the operation is performed only on those data items for which the condition is true. Branching is more costly on modern multi-issue computers than it was on the computers of the 70s.

The Hacker’s Delight book, in Chapter 6 “Find First 0-Byte”, describes both of the above approaches using 32-bits words. The first method is attributed to Leslie Lamport because he uses similar tricks in his paper. The second method was proposed by Alan Mycroft on comp.arch newsgroup in 1987.

Let’s try to understand the Mycroft’s version.

private static int firstFirstSemicolon(long word) {
    long match = word ^ 0x3B3B3B3B3B3B3B3BL;
    long mask = (match - 0x0101010101010101L) & ~match & 0x8080808080808080L;
    return Long.numberOfTrailingZeros(mask) >>> 3;
}
  • 0x3B is our pattern, it is ';' in ASCII
  • word ^ 0x3B will set all matching ';' bytes in word to 0x00
  • (x - 0x01) converts all 0x00 bytes to 0xFF, sets the highest bit of a byte to 1
    • It converts the set of { 0x00, 0x81, 0x82, 0x83, ..., 0xFF } bytes into { 0xFF, 0x80, 0x81, 0x82, ..., 0xFE } set.
  • ~x converts all 0x00 bytes to 0xFF, sets the highest bit of a byte to 1
    • Similarly, this instruction converts { 0x00, 0x01, 0-x02, 0x03, ..., 0xFF } byte set into { 0xFF, 0xFE, 0xFD, 0xFC, ..., 0x80 } set.
  • (x - 0x01) & ~x will retain the highest set bit of byte, only if the byte is 0x00
    • Since both above input sets contain 0x00, applying bitwise AND on both sets will keep the highest bit set only for the 0x00 byte.
  • 0x80 then zeros all bits except the highest bit of each byte
  • By counting number of trailing zeros, we find the index of first 0x00 byte

This is nice explanation from “Detects zero bytes inside a 32 bit integer” article.

Java Vector API

The second optimization is to use the Java Vector API for finding index of the first matching pattern in a byte array.

Java Vector API is a preview feature in Java 21 that enable developers to take advantage of Single Instruction Multiple Data (SIMD) processors. Instead of depending on Java autovectorization, by using Vector API you tell the compiler to take advantage of the SIMD instructions.

To see how to use Java Vector API, let us calculate the norm of two arrays. The scalar implementation will be as following:

// Assuming arrays are of the same length
void scalarNormComputation(float[] a, float[] b, float[] c) {
    for (int i = 0; i < a.length; i++) {
        c[i] = (a[i] * a[i] + b[i] * b[i]) * -1.0f;
    }
}

And a possible vectorized implementation:

static final VectorSpecies<Float> SPECIES = FloatVector.SPECIES_PREFERRED;

void vectorNormComputation(float[] a, float[] b, float[] c) {
    int i = 0;
    int upperBound = SPECIES.loopBound(a.length);
    for (; i < upperBound; i += SPECIES.length()) {
        var va = FloatVector.fromArray(SPECIES, a, i);
        var vb = FloatVector.fromArray(SPECIES, b, i);
        var vc = va.mul(va).add(vb.mul(vb)).neg();
        vc.intoArray(c, i);
    }
    for (; i < a.length; i++) {
        c[i] = (a[i] * a[i] + b[i] * b[i]) * -1.0f;
    }
}

At the end, we perform calculation for the leftover elements that are not included in the vectorized loop.

Similar to norm computation, we can check equality (single instruction) of semicolon ; on multiple bytes at once using Vector API.

An example from Yevhenii Melnyk submission (slightly modified by me):

private static final byte SEMICOLON = ';';
private static final VectorSpecies<Byte> BYTE_SPECIES = ByteVector.SPECIES_PREFERRED;
private static final int BYTE_SPECIES_BYTE_SIZE = BYTE_SPECIES.vectorByteSize();
private static final Vector<Byte> SEMICOLON_VECTOR = BYTE_SPECIES.broadcast(SEMICOLON);

// Finds the position of first semicolon in the given byte array
private static int findDelimiter(BufferedFile file, int startPos) {
    int position = startPos;
    int vectorLoopBound = startPos + BYTE_SPECIES.loopBound(file.bufferLimit - startPos);
    for (; position < vectorLoopBound; position += BYTE_SPECIES_BYTE_SIZE) {
        var vector = ByteVector.fromArray(BYTE_SPECIES, file.buffer, position);
        var comparisonResult = vector.compare(VectorOperators.EQ, SEMICONLON_VECTOR);
        if (comparisonResult.anyTrue()) {
            return position + comparisonResult.firstTrue();
        }
    }

    while (file.buffer[position] != SEMICOLON) {
        position++;
    }

    return position;
}

Conclusion

I have also run these methods through JMH benchmarks. GitHub repository with the code and benchmarks is morazow/java-simd-benchmarks.

The benchmark evaluates the average running time (lower is faster) of each method on randomly generated 100K and 100M measurements data.

Evaluation of finding semicolons in 100K measurements data. Evaluation of finding semicolons in 100M measurements data. 
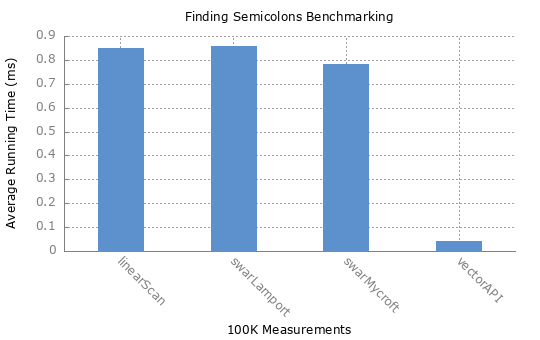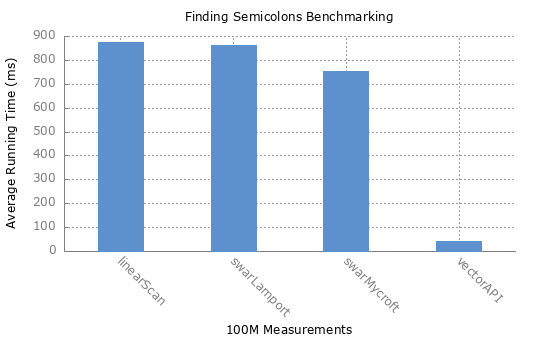Benchmark                                         (filename)  Mode  Cnt       Score       Error  Units
FindingSemicolonBenchmark.linearScan   measurements-100K.txt  avgt   10     831,308 ±     5,847  us/op
FindingSemicolonBenchmark.swarLamport  measurements-100K.txt  avgt   10     837,476 ±     6,740  us/op
FindingSemicolonBenchmark.swarMycroft  measurements-100K.txt  avgt   10     755,864 ±     6,198  us/op
FindingSemicolonBenchmark.vectorAPI    measurements-100K.txt  avgt   10      41,236 ±     0,827  us/op
FindingSemicolonBenchmark.linearScan   measurements-100M.txt  avgt   10  850736,385 ± 13573,874  us/op
FindingSemicolonBenchmark.swarLamport  measurements-100M.txt  avgt   10  847787,746 ± 24557,818  us/op
FindingSemicolonBenchmark.swarMycroft  measurements-100M.txt  avgt   10  767232,577 ± 19555,154  us/op
FindingSemicolonBenchmark.vectorAPI    measurements-100M.txt  avgt   10   42925,814 ±  1993,941  us/op

Benchmark is run using OpenJDK 21 Temurin, on Apple M2 Pro with 12 (8 performance and 4 efficiency) CPU cores and 16 GB memory.

The linear scan method having similar running time as first SWAR method could be explained by the fact that branch predictor learning the benchmark data. The Java Vector API implementation runs the fastest.

In this post we only looked at a couple of the optimizations. There are many other interesting techniques that were used by the participants. The challenge was fun and great learning experience.

Thanks a lot Gunnar for your efforts and time organizing it!

References